Cách tìm giá trị nhỏ nhất - tìm giá trị lớn nhất, nhỏ nhất của một biểu thức
Tài liệu Giáo viên
Lớp 2Lớp 2 - kết nối tri thức
Lớp 2 - Chân trời sáng sủa tạo
Lớp 2 - Cánh diều
Tài liệu Giáo viên
Lớp 3Lớp 3 - kết nối tri thức
Lớp 3 - Chân trời sáng tạo
Lớp 3 - Cánh diều
Tài liệu Giáo viên
Lớp 4Sách giáo khoa
Sách/Vở bài bác tập
Tài liệu Giáo viên
Lớp 5Sách giáo khoa
Sách/Vở bài bác tập
Tài liệu Giáo viên
Lớp 6Lớp 6 - kết nối tri thức
Lớp 6 - Chân trời sáng tạo
Lớp 6 - Cánh diều
Sách/Vở bài tập
Tài liệu Giáo viên
Lớp 7Lớp 7 - kết nối tri thức
Lớp 7 - Chân trời sáng sủa tạo
Lớp 7 - Cánh diều
Sách/Vở bài tập
Tài liệu Giáo viên
Lớp 8Sách giáo khoa
Sách/Vở bài xích tập
Tài liệu Giáo viên
Lớp 9Sách giáo khoa
Sách/Vở bài xích tập
Tài liệu Giáo viên
Lớp 10Lớp 10 - kết nối tri thức
Lớp 10 - Chân trời sáng tạo
Lớp 10 - Cánh diều
Sách/Vở bài tập
Tài liệu Giáo viên
Lớp 11Sách giáo khoa
Sách/Vở bài bác tập
Tài liệu Giáo viên
Lớp 12Sách giáo khoa
Sách/Vở bài bác tập
Tài liệu Giáo viên
giáo viênLớp 1
Lớp 2
Lớp 3
Lớp 4
Lớp 5
Lớp 6
Lớp 7
Lớp 8
Lớp 9
Lớp 10
Lớp 11
Lớp 12

Lý thuyết, các dạng bài tập Toán 8Toán 8 Tập 1I. định hướng & trắc nghiệm theo bài
II. Các dạng bài xích tập
Toán 8 Tập 1I. định hướng & trắc nghiệm theo bài xích học
II. Những dạng bài tập
Cách tìm giá chỉ trị lớn nhất, giá bán trị nhỏ tuổi nhất của phân thức cực hay, bao gồm đáp án
Trang trước
Trang sau
Cách tìm giá chỉ trị khủng nhất, giá bán trị bé dại nhất của phân thức cực hay, tất cả đáp án
A.Phương pháp giải
1.Cho biểu thức f(x,y..). Ta nói M là giá bán trị lớn số 1 (GTLN) của biểu thức f(x, y, ..) kí hiệu max f = M nếu thỏa mãn nhu cầu hai điều kiện sau đây
(1)với hầu hết x, y, .. Nhằm f(x, y, ..) xác định thì f(x, y, ..) ≤ M (M là hằng số)
(2)Tồn tại x0, y0,.. Thế nào cho f(x0, y0 , ..) = M
2.Cho biểu thức f(x,y..). Ta nói m là giá trị nhỏ dại nhất (GTNN) của biểu thức f(x, y, ..) kí hiệu min f = m nếu thỏa mãn nhu cầu hai điều kiện sau đây
Bài toán tìm giá trị lớn nhất (GTLN), giá trị nhỏ dại nhất (GTNN) của hàm số xuất hiện khá hay xuyên trong những đề thi toán học. Với tương đối nhiều mức độ, nhiều dạng khác nhau. đọc được sự trở ngại của học sinh khi ban đầu tiếp xúc với những dạng bài này, bài xích học từ bây giờ Verba
Learn sẽ tổng đúng theo lại cụ thể các dạng toán và kiến thức và kỹ năng liên quan cho GTLN, GTNN trong toán học và nhất là chương trình toán lớp 12.
Bạn đang xem: Cách tìm giá trị nhỏ nhất
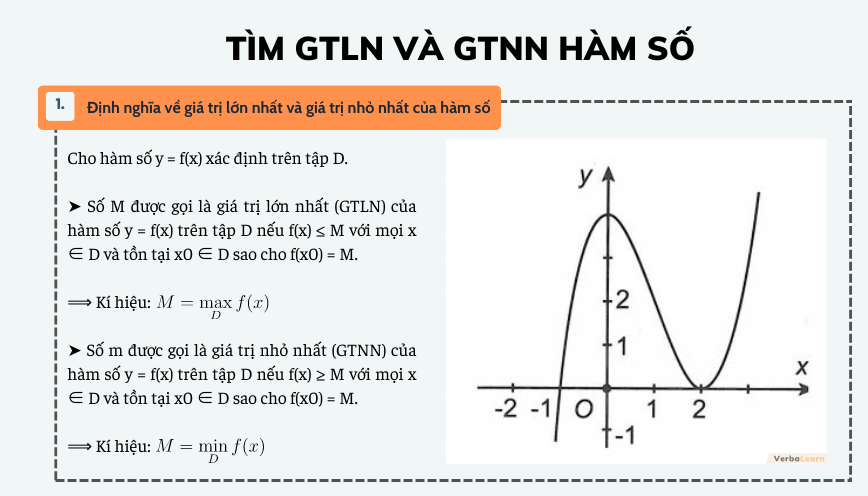
Lý thuyết giá bán trị bự nhất nhỏ nhất của hàm số
Cho hàm số y = f(x) xác định trên tập D.
+) Số M được gọi là giá bán trị lớn số 1 (GTLN) của hàm số y = f(x) bên trên tập D nếu f(x) ≤ M với mọi x ∈ D và tồn tại x0 ∈ D sao để cho f(x0) = M.
Kí hiệu:

+) Số m được gọi là giá chỉ trị nhỏ tuổi nhất (GTNN) của hàm số y = f(x) bên trên tập D ví như f(x) ≥ M với tất cả x ∈ D cùng tồn trên x0 ∈ D thế nào cho f(x0) = M.
Kí hiệu:

⟹ Sơ đồ hệ thống hóa giá chỉ trị nhỏ tuổi nhất, giá chỉ trị lớn nhất của hàm số
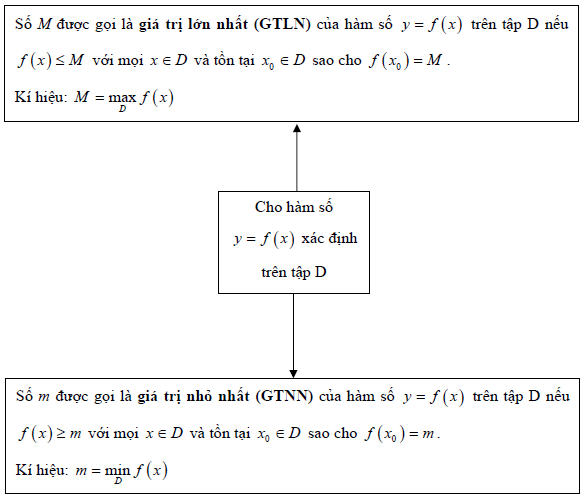
Phân dạng bài xích tập tìm kiếm GTLN GTNN của hàm số
Thông thường đối với các bài bác giảng về giá bán trị lớn số 1 giá trị nhỏ tuổi nhất chỉ có cơ phiên bản vài dạng bài bác tập. Tuy nhiên đối với một nội dung bài viết tổng quan về chuyên đề như này thì Verba
Learn tạo thành 13 dạng trường đoản cú cơ bản, vận dụng cho đến vận dụng cao. Nếu các dạng bài tập vượt dài chúng ta đọc hoàn toàn có thể tải những tài liệu về giúp thấy một cách dễ ợt hơn.
Dạng 1: Tìm giá chỉ trị bự nhất nhỏ tuổi nhất của hàm số y = f(x) bên trên một khoảng
phương thức giảiTa thực hiện các bước sau:
Bước 1. Kiếm tìm tập khẳng định (nếu đề chưa mang lại khoảng)Bước 2. Tính y’ = f’(x); tìm các điểm nhưng mà đạo hàm bằng không hoặc ko xác định.Bước 3. Lập bảng biến đổi thiênBước 4. Kết luận
Lưu ý: hoàn toàn có thể dùng máy tính cầm tay để giải theo quá trình như sau:
Bước 1. Để tìm giá bán trị khủng nhất, giá chỉ trị nhỏ tuổi nhất của hàm số y = f(x) bên trên miền (a;b) ta sử dụng máy tính Casio với lệnh MODE 7 (MODE 9 lập báo giá trị)
Bước 2. Quan tiền sát báo giá trị máy tính xách tay hiển thị, giá chỉ trị phệ nhất mở ra là max, giá bán trị nhỏ nhất lộ diện là min.
– Ta tùy chỉnh thiết lập miền quý hiếm của biến đổi x Start a end b Step

Chú ý: khi đề bài xích liên có những yếu tố lượng giác sinx, cosx, tanx… ta chuyển máy tính xách tay về cơ chế Radian.
Bài tập vận dụngCâu 1. mang đến hàm số

A.

B.
C.
D. Hàm số ko tồn tại giá trị khủng nhất
Hướng dẫn giải
Chọn B
Tập khẳng định D = ℝ
Ta bao gồm f’(x) = -2x5 + 2x4 – x + 1 = – (x – 1)(2x4 + 1)
Khi đó f’(x) = 0 ⇔ – (x – 1)(2x4 + 1) = 0 ⇔ x = 1
Bảng phát triển thành thiên
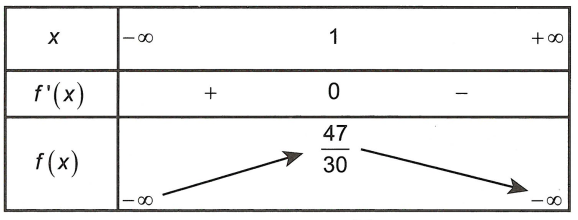
Dựa vào bảng phát triển thành thiên, ta thấy trên x = 1
Câu 2. hotline a là giá chỉ trị lớn nhất của hàm số


A.

B.

C.

D.

Hướng dẫn giải
Chọn C
Hàm số liên tục trên khoảng tầm (-∞; 1)
Ta gồm

Khi kia f’(x) = 0 ⇔ 8x2 – 12x – 8 = 0 ⇔

Bảng trở nên thiên
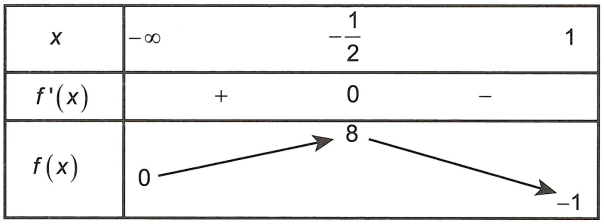
Dựa vào bảng thay đổi thiên, ta thấy

Câu 3. cho hàm số

A.

B.
C.

D. Hàm số không có giá trị nhỏ dại nhất
Hướng dẫn giải
Chọn B
Tập xác minh D = ℝ
Ta gồm


Do đó y’ = 0 ⇔ 2x2 – 2 = 0 ⇔ x = ±1
Bảng trở thành thiên
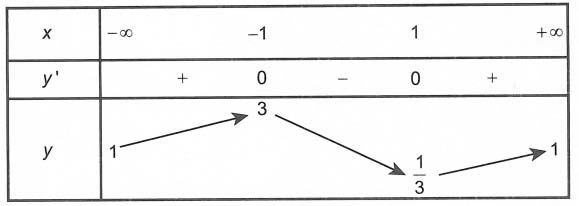
Dựa vào bảng trở thành thiên, ta thấy trên x = 1
Dạng 2: Tìm giá bán trị khủng nhất nhỏ tuổi nhất của hàm số bên trên một đoạn
phương pháp giải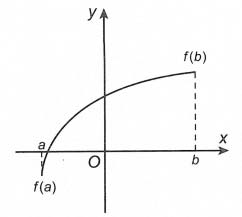
Bước 3. Tính f(a), f(xi), f(b)Bước 4. Kiếm tìm số lớn số 1 M cùng số nhỏ tuổi nhất m trong những số trên.
Khi đó


Chú ý:
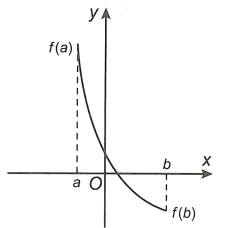
– Hàm số y = f(x) đồng trở thành trên đoạn 
– Hàm số y = f(x) nghịch thay đổi trên đoạn 
Câu 1. đến hàm số


A. 16
B.

C.

D.

Hướng dẫn giải
Chọn D
Ta bao gồm

⇒ Hàm số nghịch phát triển thành trên <2; 3>.
Do đó

Vậy

Câu 2. call M, m lần lượt là giá bán trị lớn nhất và nhỏ tuổi nhất của hàm số

A.

B.

C.

D.

Hướng dẫn giải
Chọn A
Tập xác minh D = <-2; 2>
Ta gồm

y’ = 0 ⇔


Vậy

Câu 3. giá bán trị nhỏ dại nhất của hàm số y = 2x3 – 3x2 + m trên đoạn <0; 5> bằng 5 lúc m bằng
A. 6
B. 10
C. 7
D. 5
Hướng dẫn giải
Chọn A.
Hàm số xác minh và tiếp tục trên D = <0; 5>
Ta gồm y’ = 0 ⇔ 6x2 – 6x = 0 ⇔

f (0) = m; f (1) = m – 1; f (5) = 175 + m
Dễ thấy f (5) > f (0) > f (1), ∀ m ∈ ℝ yêu cầu

Theo đề bài

Câu 4. điện thoại tư vấn A, B là giá bán trị nhỏ dại nhất, giá chỉ trị lớn số 1 của hàm số


A. M = 1; m = -2
B. M = -2
C. M = ±2
D. M = -1; m = 2
Hướng dẫn giải
Chọn A
Hàm số đang cho tiếp tục trên đoạn <2; 3>
Ta có


Do kia

⇔ 3m2 + m – 6 = 0 ⇔

Câu 5. Biết hàm số y = x3 + 3mx2 + 3(2m – 1) x + 1 (với m là tham số) trên đoạn <-2; 0> đạt giá bán trị lớn số 1 bằng 6. Những giá trị của tham số m là
A. M = 1
B. M = 0
C. M = 3
D. M = -1
Hướng dẫn giải
Chọn D
y’ = 0 ⇔

Vì y(-2) = -1; y(0) = 1 với theo bài ra

Do đó giá trị lớn nhất đạt trên y(-1) hoặc y(1 – 2m).
Ta bao gồm y(-1) = -3m + 3; y(1 – 2m) = (1 – 2m)2(m – 2) + 1
Trường đúng theo 1: Xét -3m + 3 = 6 ⇔ m = -1
Thử lại với m = -1, ta bao gồm y’ = 0 ⇔

Trường hòa hợp 2: Xét

Vì

Thực hiện theo công việc sau
– bước 1. Tìm giá chỉ trị khủng nhất, giá chỉ trị nhỏ dại nhất của hàm số f(x) trên đoạn
– bước 2.
+) search

+) tìm kiếm

Trường đúng theo 1: M․m bài tập vận dụng
Câu 1. giá chỉ trị bé dại nhất của hàm số y = |x3 – 9x2 + 24x – 68| bên trên đoạn <-1; 4> bằng
A. 48
B. 52
C. -102
D. 0
Hướng dẫn giải
Chọn A
Bảng biến hóa thiên của hàm số y = x3 – 9x2 + 24x – 68 bên trên đoạn <-1; 4>
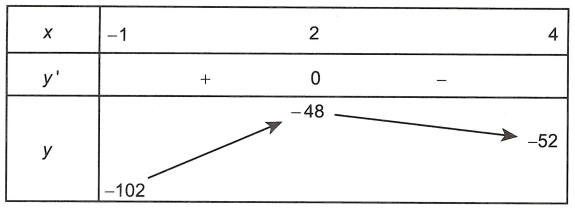
Suy ra bảng vươn lên là thiên của hàm số y = |x3 – 9x2 + 24x – 68| trên đoạn <-1; 4> là
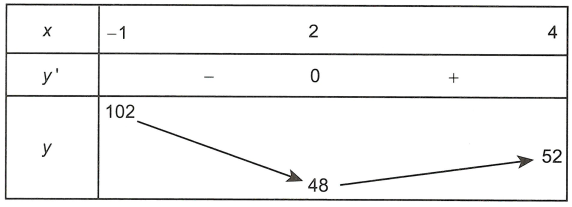
Vậy giá bán trị nhỏ nhất của hàm số y = |x3 – 9x2 + 24x – 68| trên đoạn <-1; 4> bởi 48.
Cách khác: Theo trường phù hợp 3 thì M = -48 4 – 14x2 + 48x + m – 30| bên trên đoạn <0; 2> ko vượt quá 30. Tổng các bộ phận của S bằng
A. 108
B. 120
C. 210
D. 136
Hướng dẫn giải
Chọn D
Xét hàm số g(x) = ¼ x4 – 14x2 + 48x + m – 30 trên đoạn <0; 2>
Ta tất cả g’(x) = x3 – 28x + 48 ⇒ g’(x) = 0 ⇔

Để

⇒ m ∈ 0; 1; 2; …; 15; 16
Tổng các bộ phận của S là 136.
Câu 4. Biết giá trị lớn nhất của hàm số

Mệnh đề nào dưới đây đúng?
A. 0 cách thức giải
Thực hiện các bước sau
– bước 1. Tìm

– cách 2. Hotline M là giá bán trị lớn số 1 của số y = |f(x) + g(m)| thì
M = max≥

Dấu bằng xẩy ra khi và chỉ còn khi |α + g(m)| = |β + g(m)|
Áp dụng bất đẳng thức

Dấu bằng xảy ra khi còn chỉ khi <α + g(m)>․<β + g(m)> ≥ 0
– bước 3. Tóm lại


Câu 1. biết rằng giá trị lớn nhất của hàm số y = |x2 + 2x + m – 4| bên trên đoạn <-2; 1> đạt giá trị bé dại nhất, cực hiếm của thông số m bằng
A. 1
B. 3
C. 4
D. 5
Hướng dẫn giải
Chọn B
Đặt f(x) = x2 + 2x
Ta bao gồm f’(x) = 2x + 2
f’(x) = 0 ⇔ x = -1 ∈ <-2; 1>
f (-2) = 0; f (1) = 3; f (-1) = -1
Do kia

Suy ra

Dấu bằng xẩy ra khi còn chỉ khi

Câu 2. Để giá chỉ trị lớn nhất của hàm số

A.
B.

C.

D.

Hướng dẫn giải
Chọn A
Tập xác minh D = <0; 2>
Đặt

Ta tất cả

f (0) = 0; f (2) = 0; f (1) = 1
Suy ra


Dấu bằng xảy ra ⇔

Suy trả giá trị lớn số 1 của hàm số là nhỏ nhất lúc
Câu 3. giá bán trị nhỏ dại nhất của hàm số y = f (x, m) = |x2 – 2x + 5| + mx đạt giá bán trị lớn nhất bằng
A. 2
B. 5
C. 8
D. 9
Hướng dẫn giải
Chọn B
Ta tất cả min f (x, m) ≤ f (0, m) = 5, ∀ m ∈ ℝ
Xét m = 2 ta có f (x, 2) = |x2 – 2x + 5| + 2x ≥ x2 – 2x + 5 + 2x ≥ 5, ∀ x ∈ ℝ
Dấu bằng xẩy ra tại x = 0. Suy ra min f (x, 2) = 5, ∀ x ∈ ℝ
Do kia

Tổng quát: y = |ax2 + bx + c| + mx
Trường vừa lòng 1: a․c > 0 ⇒ max (miny) = c
Đạt được lúc m = -b
Câu 4. giá bán trị nhỏ nhất của hàm số f (x, m) = |x2 – 4x – 7| đạt giá trị lớn số 1 bằng
A. 7
B. -7
C. 0
D. 4
Hướng dẫn giải
Chọn C
Phương trình x2 – 4x – 7 luôn có hai nghiệm trái dấu x1 2
– Trường hợp 1: trường hợp m ≥ 0
Ta gồm min f (x, m) ≤ f (x1, m) = mx1 ≤ 0, ∀ m ∈ ℝ
Xét m = 0 ta có f (x, 0) = |x2 – 4x – 7| ≥ 0, ∀ x ∈ ℝ
Dấu bằng xảy ra tại x = x1, 2. Suy ra min f (x, m) = 0, ∀ x ∈ ℝ
Do đó

– Trường hòa hợp 2: nếu m 2, m) = mx2
Câu 1. Hàm số y = f(x) liên tục trên ℝ và tất cả bảng thay đổi thiên như hình bên dưới
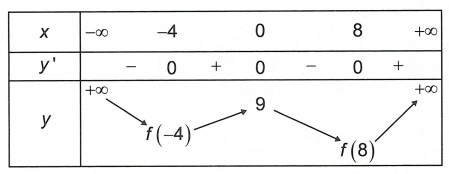
Biết f (-4) > f (8), khi ấy giá trị nhỏ tuổi nhất của hàm số đã mang đến trên ℝ bằng
A. 9
B. F (-4)
C. F (8)
D. -4
Hướng dẫn giải
Chọn C
Từ bảng trở nên thiên ta bao gồm f(x) ≥ f (-4) ∀ m ∈ (-∞; 0> cùng f(x) ≥ f (8), ∀ m ∈ (0; +∞)
Mặt khác f (-4) > f (8) suy ra x ∈ (-∞; +∞) thì f(x) ≥ f (8)
Vậy

Câu 2. mang lại hàm số y = f(x) xác minh trên tập hợp

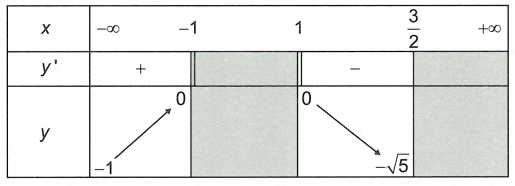
Khẳng định đúng là
A. ; không tồn tại

B. ;

C. ;

D.


Hướng dẫn giải
Chọn B
Dựa vào bảng phát triển thành thiên thì

Câu 3. cho hàm số y = f(x) thường xuyên trên đoạn <-1; 3> và có đồ thị như hình vẽ bên dưới.
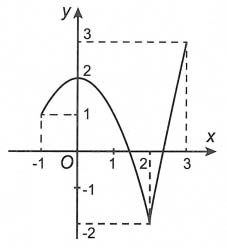
Gọi M cùng m lần lượt là giá chỉ trị lớn số 1 và nhỏ dại nhất của hàm số đã mang đến trên đoạn <-1; 3>. Cực hiếm của M – m bằng
A. 1
B. 3
C. 4
D. 5
Hướng dẫn giải
Chọn D
Dựa vào vật thị suy ra
M = f (3) = 3; m = f (2) = -2
Vậy M – m = 5
Câu 4. đến đồ thị hàm số y = f’(x) như hình vẽ
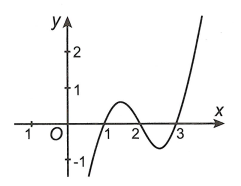
Hàm số y = f(x) đạt giá bán trị lớn nhất trên khoảng chừng <1; 3> trên x0. Khi ấy giá trị của x02 – 2x0 + 2019 bởi bao nhiêu?
A. 2018
B. 2019
C. 2021
D. 2022
Hướng dẫn giải
Chọn B
Dựa vào vật thị của hàm số y = f’(x) ta có bảng thay đổi thiên như sau
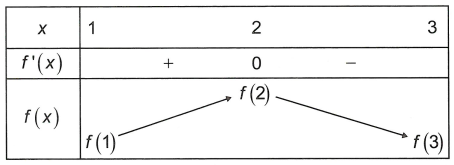
Dựa vào bảng trở nên thiên suy ra hàm số y = f(x) đạt giá chỉ trị lớn nhất trên khoảng chừng <1; 3> trên x0 = 2
Vậy x02 – 2x0 + 2019 = 2019
Dạng 6. Tìm giá trị bự nhất, giá bán trị nhỏ dại nhất của hàm con số giác
cách thức giảiGhi nhớ: Điều kiện của các ẩn phụ
– giả dụ

– nếu như

– nếu

Nếu t = sinx ± cosx =

Bước 2. Giải bài toán tìm giá chỉ trị phệ nhất, giá bán trị nhỏ nhất của hàm số theo ẩn phụ
Bước 3. Tóm lại (Chọn đáp án)Bài tập vận dụng
Câu 1. Xem thêm: Hướng dẫn cách đăng ảnh và video cùng lúc lên facebook mới nhất
A. ; m = -4
B. M = 4; m = 0
C. M = 0;
D. M = 4;
Hướng dẫn giải
Chọn A
Ta bao gồm y = 2cos2x + 2sinx = 2(1 – 2sin2x) + 2sinx = -4sin2x + 2sinx + 2
Đặt t = sin x, t ∈ <-1; 1>, ta được y = -4t2 + 2t +2
Ta có y’ = 0 ⇔ -8t + 2 = 0 ⇔ t = ¼ ∈ (-1; 1)
Vì

Câu 2. Tổng giá trị lớn nhất và giá trị bé dại nhất của hàm số

A.
B.

C.

D. 3
Hướng dẫn giải
Chọn B
Đặt t = |cosx| ⇒ 0 ≤ t ≤ 1, ta được

Vì


Suy ra tổng giá bán trị lớn số 1 và giá trị nhỏ nhất của hàm số đã mang đến bằng

Câu 3. giá chỉ trị lớn số 1 M của hàm số

A.
B. M = 3
C.

D.

Hướng dẫn giải
Chọn A
Đặt t = cos2x ⇒ 0 ≤ t ≤ 1, ta được

Ta gồm

Vì

Câu 4. đến hàm số

A.

B.

C.
D.

Hướng dẫn giải
Chọn A
Xét

Đặt t = sinx ⇒ -1 ≤ t ≤ 1, ta được

Ta tất cả

Vì


Hay

Mặt không giống

Do kia


Dấu bằng đã đạt được khi

Câu 5. giá bán trị bé dại nhất của biểu thức p = |1 + 2cosx| + |1 + 2sinx| bằng
A.

B.

C. 1
D.

Hướng dẫn giải
Chọn B
Ta tất cả P2 = 6 + 4(sinx + cosx) + 2|1 + 2(sinx + cosx) + 4sinx․cosx|
Đặt t = sinx + cosx =


Xét y = P2 = 6 + 4t + 2 |2t2 + 2t – 1| =


Bảng biến đổi thiên
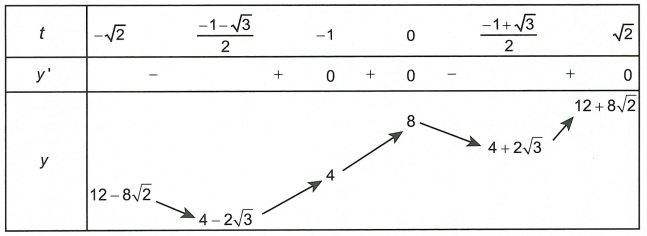
Dựa vào bảng biến đổi thiên, suy ra

Câu 6. giá chỉ trị lớn số 1 của hàm số f(x) = sinx + cos2x trên đoạn <0; π> là
A.

B.

C.

D.
Hướng dẫn giải
Chọn D
Đặt t = sinx ⇒ cos2x = 1 – 2sin2x = 1 – 2t2 , với x ∈ <0; π> ⇒ t ∈ <0; 1>
Ta được f(t) = -2t2 + t + 1 cùng với t ∈ <0; 1>
Ta tất cả f’(t) = -4t + 1 = 0 ⇔ t = ¼ ∈ (0; 1)
Do f (0) = 1;


Vậy giá bán trị lớn nhất của hàm số là
Dạng 7. Tìm giá chỉ trị lớn nhất, giá bán trị nhỏ dại nhất của hàm số khác
Câu 1. giá bán trị lớn số 1 của hàm số

A.

B. -5
C.

D. 3
Hướng dẫn giải
Chọn A
Do

Đặt

Khi đó y = 4t3 + 6t – 1 với t ∈
Vì y’ = 12t2 + 6 > 0, ∀ t yêu cầu hàm số đồng trở thành trên
Do kia

Câu 2. giá bán trị khủng nhất, giá bán trị nhỏ tuổi nhất của hàm số

A. 2;

B. 4; 2
C. 4;
D. 4;
Hướng dẫn giải
Chọn D
Tập xác định D = <1; 9>
Ta gồm

Vì y (1) = y (9) = ; y (5) = 4 yêu cầu max y = 4; min y = .
Nhận xét: cùng với hàm số


Suy ra

Câu 3. giá bán trị bé dại nhất của hàm số

A.
B. -2
C. -4
D. 2
Hướng dẫn giải
Chọn A
Tập khẳng định của hàm số là D = <-1; 3>
Đặt


Do

Bài toán quy về tìm giá trị lớn nhất, giá bán trị nhỏ tuổi nhất của hàm số

Ta có g’(t) = t + 1 = 0 ⇔ t = -1 ∈ (-2; 2)
Lại bao gồm g (-2) = -2; g (2) = 2; g (-1) =
Suy trả giá trị bé dại nhất bằng
Nhận xét: cùng với hàm số


Dạng 8. Tìm giá trị mập nhất, giá trị bé dại nhất của biểu thức các biến
Câu 1. đến biểu thức

A. 3
B.
C. 1
D. 4
Hướng dẫn giải
Chọn B.
Nếu y = 0 thì p. = 1 (1)
Nếu y ≠ 0 thì

Đặt



Bảng biến thiên
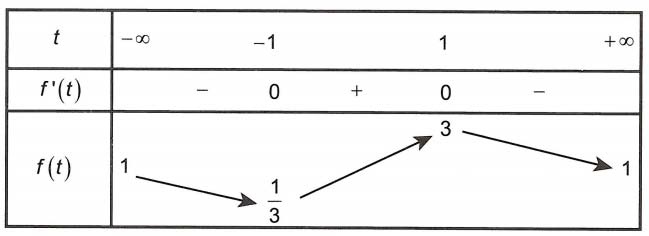
Dựa vào bảng biến đổi thiên ta có p = f(t) ≥ (2)
Từ (1) và (2) suy ra có p. = f(t) ≥ ⇒ min p =
Câu 2. mang đến hai số thực x, y thỏa mãn nhu cầu x ≥ 0, y ≥ 0 và x + y = 1. Giá bán trị nhỏ dại nhất và giá trị lớn nhất của biểu thức

A.

B. 0 cùng 1
C.

D. 1 cùng 2
Hướng dẫn giải
Chọn C
Ta tất cả


Đặt t = xy ta được

Vì x ≥ 0, y ≥ 0 ⇒ t ≥ 0
Mặt khác

Khi đó, bài toán trở thành tìm giá chỉ trị lớn nhất của hàm số trên
Xét hàm số xác minh và thường xuyên trên
Ta tất cả


⇒ Hàm số g(t) nghịch biến hóa trên đoạn
Do kia

Câu 3. đến x, y là những số thực thỏa mãn (x – 3)2 + (y – 1)2 = 5. Giá trị nhỏ nhất của biểu thức

A. 3
B.

C.
D.

Hướng dẫn giải
Chọn A
(x – 3)2 + (y – 1)2 = 5 ⇒ x2 + y2 – 6x – 2y + 5 = 0

Đặt t = x + 2y
(12 + 22)․<(x – 3)2 + (y – 1)2> ≥ <(x – 3) + (2y – 2)>2
Ta được

Xét

Vì f (0) = 4; f (10) = ; f (1) = 3 ⇒ min phường = 3 khi t = 1.
Câu 4. call x0, y0, z0 là ba số thực dương làm thế nào cho biểu thức đạt giá trị nhỏ dại nhất.
Tổng x0 + y0 + z0 bằng
A. 3
B. 1
C.

D.

Hướng dẫn giải
Chọn B
Ta có

Đặt x + y + x = t. Lúc ấy

Ta bao gồm

Bảng thay đổi thiên
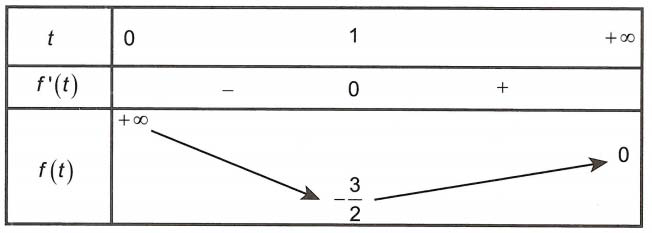
Suy ra


Do kia

Câu 5. cho x,y là những số thực dương thỏa mãn nhu cầu điều kiện

A. 8
B. 0
C. 12
D. 4
Hướng dẫn giải
Chọn B
Với điều kiện bài toán x, y > 0 và x2 – xy + 3 = 0

Lại tất cả


Từ kia

Xét hàm số

Suy ra hàm số đồng phát triển thành trên

⇒ f (1) ≤ f(x) ≤

Câu 6. đến x, y, z là bố số thực ở trong đoạn <1; 9> cùng x ≥ y, x ≥ z. Giá chỉ trị nhỏ dại nhất của biểu thức

A.

B.

C.

D. 1
Hướng dẫn giải
Chọn C
Thật vậy

Dấu bằng xẩy ra khi và chỉ còn khi a = b hoặc ab = 1.
Áp dụng bất đẳng thức trên

Đặt



f’(t) = 0 ⇔ t4 – 2t3 – 24t2 – 2t + 100 = 0
⇔ (t – 2)(t3 – 24t – 50) = 0 ⇔ t = 2 bởi vì t3 – 24t – 50 Phương pháp
Thực hiện nay theo 1 trong hai cách
Cách 1:
Bước 1. Đặt t = u(x).
Đánh giá quý giá của t trên khoảng K.
Chú ý: hoàn toàn có thể sử dụng khảo sát điều tra hàm số, bất đẳng thức để đánh giá giá trị của t = u(x).
– cách 2. Từ bỏ bảng biến thiên hoặc đồ gia dụng thị của hàm số đến ta giá bán trị lớn số 1 và giá trị bé dại nhất của hàm số y = f(t).
– cách 3. Kết luận.
Cách 2:
– cách 1. Tính đạo hàm y’ = u’(x)․f’(u(x)).
– cách 2. Tìm nghiệm y’ = u’(x)․f’(u(x)) = 0
– cách 3. Lập bảng đổi thay thiên
– cách 4. Kết luận về giá chỉ trị khủng nhất, giá trị nhỏ dại nhất của hàm số y = f(x), y = f(u(x)), y = f(u(x)) ± h(x)…
Bài tập vận dụngCâu 1. đến hàm số y = f(x) gồm bảng trở nên thiên như sau
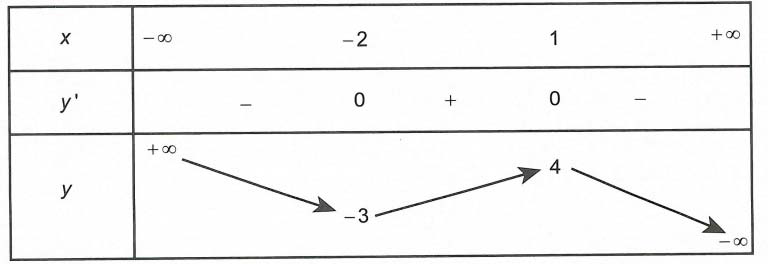
Hàm số y = f (|x – 1|) có giá trị bé dại nhất trên đoạn <0; 2> bằng
A. F (-2)
B. F (2)
C. F (1)
D. F (0)
Hướng dẫn giải
Chọn D
Đặt t =|x – 1|, ∀ x ∈ <0; 2> ⇒ t ∈ <0; 1>
Dựa vào bảng biến thiên ta tất cả hàm số y = f(t) có giá trị nhỏ nhất

Câu 2. đến hàm số y = f(x) có đồ thị như hình mẫu vẽ sau. Khi ấy hàm số y = f (2 – x2) đạt giá trị bé dại nhất bên trên bằng
A. F (-2)
B. F (2)
C. F (1)
D. F (0)
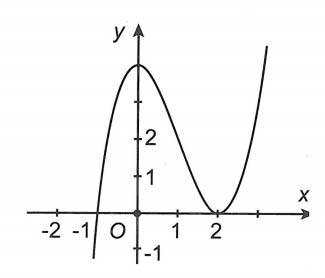
Hướng dẫn giải
Chọn B
Đặt t = 2 – x2. Trường đoản cú x ∈ ⇔ 0 ≤ x2 ≤ 2 ⇔ 2 ≥ 2 – x2 ≥ 0 ⇒ t ∈ <0; 2>
Dựa vào trang bị thị, hàm số y = f(t) có giá trị bé dại nhất

Câu 3. mang lại hàm số y = f(x) = ax4 + bx2 + c xác định và liên tục trên ℝ và bao gồm bảng phát triển thành thiên sau
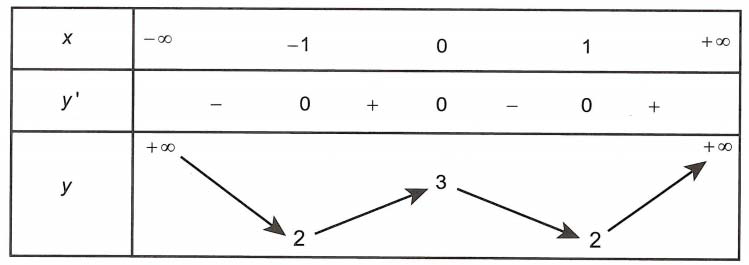
Giá trị nhỏ tuổi nhất của hàm số y = f (x + 3) bên trên đoạn <0; 2> là
A. 64
B. 65
C. 66
D. 67
Hướng dẫn giải
Chọn C
Hàm số tất cả dạng f(x) = ax4 + bx2 + c. Từ bảng biến hóa thiên ta có

⇒ f(x) = x4 – 2x2 + 3
Đặt t = x + 3, x ∈ <0; 2> ⇒ t ∈ <3; 5>
Dựa vào thiết bị thị, hàm số y = f(t) đồng phát triển thành trên đoạn <3;5>.
Do kia

Dạng 10. Tìm giá trị béo nhất, giá bán trị bé dại nhất của hàm số y = f(u(x)), y = f(u(x)) ± h(x)… lúc biết đồ thị của hàm số y = f’(x)
Câu 1. mang lại hàm số y = f(x) bao gồm đạo hàm và liên tiếp trên ℝ. Biết rằng đồ thị hàm số y = f’(x) như dưới đây.
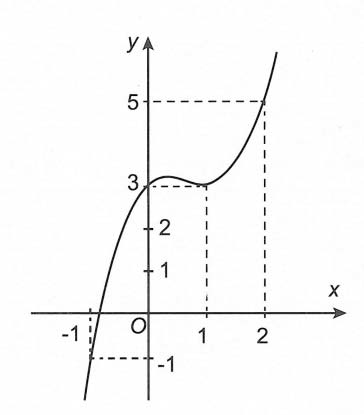
Lập hàm số g(x) = f(x) – x2 – x.
Mệnh đề nào tiếp sau đây đúng?
A. G(-1) > g(1)
B. G(-1) = g(1)
C. G(1) = g(2)
D. G(1) > g(2)
Hướng dẫn giải
Chọn D
Ta tất cả g’(x) = f’(x) – 2x – 1
Từ đồ vật thị hàm số y = f’(x) và mặt đường thẳng y = 2x + 1 ta gồm g’(x) = 0
⇔ f’(x) = 2x + 1 ⇒

Bảng vươn lên là thiên
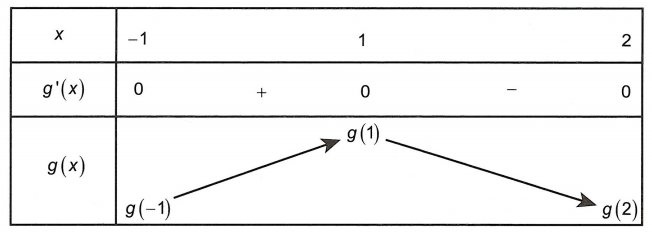
Ta chỉ cần so sánh bên trên đoạn <-1; 2>. Đường trực tiếp y = 2x + 1 là đường thẳng đi qua những điểm A(-1; -1), B(1; 3), C(2; 5) đề nghị đồ thị hàm số y = f’(x) và con đường thẳng y = 2x + 1 giảm nhau trên 3 điểm.
Dạng 11. Ứng dụng của giá bán trị lớn số 1 và nhỏ dại nhất trong những bài toán thực tế
Câu 1. Một chất điểm vận động theo quy nguyên lý s = 3t2 – t3. Thời khắc t (giây) nhưng mà tại đó gia tốc v (m/s) của hóa học điểm hoạt động đạt giá trị lớn số 1 là
A. T = 2s
B. T = 5s
C. T = 1s
D. T =3s
Hướng dẫn giải
Chọn C
Ta tất cả v(t) = s’(t) = 6t – 3t2 ⇒ v(t) = -3(t – 1)2 + 3 ≤ 3, ∀ t ∈ ℝ
Giá trị lớn nhất của v(t) = 3 lúc t = 1.
Câu 2. Một vật vận động theo quy điều khoản s = -⅓t3 + 6t2 với t (giây) là khoảng thời hạn tính từ lúc vật bước đầu chuyển đụng và s (mét) là qu









